Detaljeret analyse af RC -serien kredsløb
2024-05-08
20505
RC -seriens kredsløb, der består af en modstand og en kondensator, fungerer som en grundlæggende komponent i både basale og avancerede elektroniske systemdesign.Det hjælper med at forstå centrale principper såsom frekvensrespons, faseskift og signalfiltrering, der spiller en betydelig rolle i kredsløbsdesign og signalbehandling.Denne efterforskning dækker teoretiske grundlæggende og udvider til praktiske anvendelser gennem eksperimenter og simuleringer.Ved fysisk at samle kredsløbet eller modellere det digitalt, kan eleverne visuelt forstå opladningsprocessen og virkningerne af komponent V ariat -ioner, hvilket gør komplekse koncepter mere tilgængelige og mindeværdige.
Katalog

Figur 1: Forskellige udgangsspændinger for RC -kredsløb
Introduktion til RC -kredsløb
Et RC-kredsløb, der er kort for modstandskredsløb, er grundlæggende inden for elektronik til at manipulere signaler gennem modstande og kondensatorer.Disse kredsløb er især kendt for deres evne til at skifte faser og filtrere signaler ved hjælp af enkle arrangementer af disse komponenter.Et grundlæggende RC-kredsløb, ofte benævnt et første-ordens RC-kredsløb, inkluderer typisk kun en modstand og en kondensator.
I en typisk opsætning påføres indgangsspændingen på seriearrangementet af en modstand og en kondensator.Outputet kan trækkes enten på tværs af modstanden eller kondensatoren, der hver giver forskellige svar på signalfrekvenser på grund af kondensatorens unikke egenskaber.Denne alsidighed giver RC -kredsløb mulighed for at udføre en række roller i elektroniske enheder, såsom kobling og filtreringssignaler eller endda konvertering af bølgeformer, når de udsættes for en trinspænding.
RC-kredsløbet kan konfigureres på flere måder-serier, parallel eller en kombination af begge dele, kendt som serie-parallel.Hver konfiguration påvirker signalfrekvenser forskelligt: serieforbindelser har en tendens til at dæmpe lave frekvenser, mens parallelle forbindelser bruges til at dæmpe højere frekvenser.Denne forskel skyldes primært den måde, modstande og kondensatorer interagerer med kredsløbet;Modstande er direkte imod aktuelle, mens kondensatorer opbevarer og frigiver det, hvilket påvirker, hvordan kredsløbet reagerer på forskellige frekvenser.
I modsætning til kredsløb, der inkluderer induktorer, som LC -kredsløb, kan enkle RC -kredsløb ikke resonere, da modstande ikke opbevarer energi.Denne attribut påvirker tydeligt, hvordan RC -kredsløb bruges, med fokus på deres kapacitet til filtrering snarere end energilagring eller resonans.Hver konfiguration tjener et specifikt formål, hvilket gør RC -kredsløb alsidige værktøjer i både teoretisk undersøgelse og praktisk anvendelse i elektronisk design.
RC Series Circuit
Et RC -serien kredsløb, i det væsentlige sammensat af en modstand (R) og en kondensator (C) I serie fungerer efter et ligetil princip.Når kredsløbets switch er lukket, begynder kondensatoren at oplade fra den påførte spænding (V), der initierer en strøm af strøm gennem kredsløbet.Efterhånden som kondensatoren oplades, øges strømmen gradvist, indtil kondensatoren når sin kapacitet, på hvilket tidspunkt den holder op med at acceptere ladning, og strømmen stabiliseres til sin maksimale værdi, beregnet som 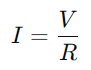 .
.
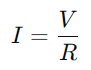 .
.Kondensatorens opladningsproces kan beskrives matematisk af ligningen 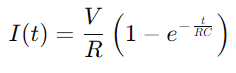 , hvor jeg er den nuværende, V er spændingen, R er modstanden, C er kapacitansen, t er tid og e er basen for den naturlige logaritme.Denne formel afspejler, hvordan de aktuelle ændrer sig over tid som kondensatoren lades med produktet af modstanden og kapacitansværdierne (RC), der definerer tidskonstantens tidskonstant, hvilket indikerer den hastighed, hvormed kondensatoren lades.
, hvor jeg er den nuværende, V er spændingen, R er modstanden, C er kapacitansen, t er tid og e er basen for den naturlige logaritme.Denne formel afspejler, hvordan de aktuelle ændrer sig over tid som kondensatoren lades med produktet af modstanden og kapacitansværdierne (RC), der definerer tidskonstantens tidskonstant, hvilket indikerer den hastighed, hvormed kondensatoren lades.
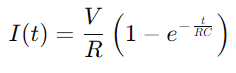 , hvor jeg er den nuværende, V er spændingen, R er modstanden, C er kapacitansen, t er tid og e er basen for den naturlige logaritme.Denne formel afspejler, hvordan de aktuelle ændrer sig over tid som kondensatoren lades med produktet af modstanden og kapacitansværdierne (RC), der definerer tidskonstantens tidskonstant, hvilket indikerer den hastighed, hvormed kondensatoren lades.
, hvor jeg er den nuværende, V er spændingen, R er modstanden, C er kapacitansen, t er tid og e er basen for den naturlige logaritme.Denne formel afspejler, hvordan de aktuelle ændrer sig over tid som kondensatoren lades med produktet af modstanden og kapacitansværdierne (RC), der definerer tidskonstantens tidskonstant, hvilket indikerer den hastighed, hvormed kondensatoren lades.
Figur 2: RC -serien kredsløb
Afskæring opstår, når kontakten åbnes, hvilket vender processen: Den lagrede energi i kondensatoren frigøres, hvilket får strømmen til at strømme i den modsatte retning, indtil kondensatoren er drænet.Denne opladnings- og afladningscyklus er afgørende i applikationer såsom signalomdannelse, filtrering og timingkredsløb på grund af den forudsigelige måde, hvorpå den nuværende og spænding ændres.

Figur 3: RC -serien kortslutning
Opførslen af RC -seriekredsløbet varierer også med frekvens.Ved lave frekvenser fungerer kondensatoren mere som et åbent kredsløb, hvilket i høj grad hindrer strømmen af strøm.Når frekvensen øges, falder den kapacitive reaktans, hvilket gør det lettere for strømmen at passere.Denne ændring i impedans med frekvens gør det muligt for RC -serien kredsløb at fungere som et filter, hvilket selektivt dæmper frekvenser under en bestemt tærskel (drejningsfrekvens  ).
).
 ).
).
Figur 4: Opladning og afladning af RC -serien kredsløb
Foruden stabilitetsoperationer studeres også RC-kredsløb for deres kortvarige svar, når de udsættes for pludselige ændringer i spænding, såsom når en DC-strømforsyning tændes eller slukkes.Dette scenarie kaldes en kortvarig proces, hvor kredsløbet overgår fra en stabil tilstand til en anden.Dynamikken i denne proces afhænger markant af RC -tidskonstanten, som styrer, hvor hurtigt kredsløbet reagerer på ændringer.
I sidste ende serverer RC -serien kredsløb flere funktioner i både DC- og AC -applikationer, hvor man håndterer opgaver, der spænder fra at forsinke signaler til integration eller kobling af forskellige kredsløbselementer.Denne alsidighed stammer fra de unikke interaktioner mellem modstanden og kondensatoren, som tilsammen bestemmer kredsløbets samlede respons på ændringer i spænding og frekvens.

Figur 5: RC -serien kredsløbsdiagram og frekvensformel
I et RC -serien kredsløb mellem modstanden (R) og kondensatoren (C) påvirker både strømstrøm og spændingsfordeling.Modstandens primære rolle er at regulere den aktuelle strømning.Dette forhold kvantificeres efter Ohms lov, der siger 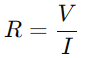 , hvor V er spænding og jeg er aktuel.I det væsentlige fungerer modstanden som en flaskehals og kontrollerer, hvor meget elektricitet der kan passere på ethvert givet tidspunkt.
, hvor V er spænding og jeg er aktuel.I det væsentlige fungerer modstanden som en flaskehals og kontrollerer, hvor meget elektricitet der kan passere på ethvert givet tidspunkt.
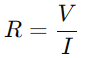 , hvor V er spænding og jeg er aktuel.I det væsentlige fungerer modstanden som en flaskehals og kontrollerer, hvor meget elektricitet der kan passere på ethvert givet tidspunkt.
, hvor V er spænding og jeg er aktuel.I det væsentlige fungerer modstanden som en flaskehals og kontrollerer, hvor meget elektricitet der kan passere på ethvert givet tidspunkt.Kondensatorens funktion er lidt mere kompliceret, da den midlertidigt opbevarer elektrisk energi og derefter frigiver den tilbage i kredsløbet.Spændingen over kondensatoren (VC) korrelerer med sin gemte afgift (Q) og beregnes ved hjælp af formlen 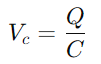 .Dette forhold fremhæver kondensatorens kapacitet til at holde opladning, hvilket direkte påvirker den spænding, den udviser.Under drift er dynamikken ved opladning og udledning af kondensatoren afgørende for at forstå RC -kredsløb.Tidskonstanten (τ), defineret som
.Dette forhold fremhæver kondensatorens kapacitet til at holde opladning, hvilket direkte påvirker den spænding, den udviser.Under drift er dynamikken ved opladning og udledning af kondensatoren afgørende for at forstå RC -kredsløb.Tidskonstanten (τ), defineret som 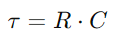 , måler, hvor hurtigt kondensatoren når ca. 63,2% af den fulde spænding, der leveres af kilden (V0).Denne tidskonstant er tegn på, hvordan kredsløbet tilpasser sig til at indtaste ændringer, med modstanden og kondensatoregenskaberne, der dikterer tempoet i disse justeringer.
, måler, hvor hurtigt kondensatoren når ca. 63,2% af den fulde spænding, der leveres af kilden (V0).Denne tidskonstant er tegn på, hvordan kredsløbet tilpasser sig til at indtaste ændringer, med modstanden og kondensatoregenskaberne, der dikterer tempoet i disse justeringer.
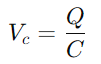 .Dette forhold fremhæver kondensatorens kapacitet til at holde opladning, hvilket direkte påvirker den spænding, den udviser.Under drift er dynamikken ved opladning og udledning af kondensatoren afgørende for at forstå RC -kredsløb.Tidskonstanten (τ), defineret som
.Dette forhold fremhæver kondensatorens kapacitet til at holde opladning, hvilket direkte påvirker den spænding, den udviser.Under drift er dynamikken ved opladning og udledning af kondensatoren afgørende for at forstå RC -kredsløb.Tidskonstanten (τ), defineret som 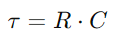 , måler, hvor hurtigt kondensatoren når ca. 63,2% af den fulde spænding, der leveres af kilden (V0).Denne tidskonstant er tegn på, hvordan kredsløbet tilpasser sig til at indtaste ændringer, med modstanden og kondensatoregenskaberne, der dikterer tempoet i disse justeringer.
, måler, hvor hurtigt kondensatoren når ca. 63,2% af den fulde spænding, der leveres af kilden (V0).Denne tidskonstant er tegn på, hvordan kredsløbet tilpasser sig til at indtaste ændringer, med modstanden og kondensatoregenskaberne, der dikterer tempoet i disse justeringer.Spændingen over kondensatoren på ethvert givet tidspunkt under ladningen gives af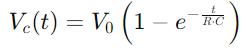 , der illustrerer en ikke-lineær stigning, når kondensatoren fylder.Denne ligning beskriver, hvordan ladningshastigheden bremser, når kondensatoren nærmer sig fuld kapacitet.
, der illustrerer en ikke-lineær stigning, når kondensatoren fylder.Denne ligning beskriver, hvordan ladningshastigheden bremser, når kondensatoren nærmer sig fuld kapacitet.
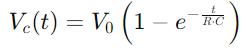 , der illustrerer en ikke-lineær stigning, når kondensatoren fylder.Denne ligning beskriver, hvordan ladningshastigheden bremser, når kondensatoren nærmer sig fuld kapacitet.
, der illustrerer en ikke-lineær stigning, når kondensatoren fylder.Denne ligning beskriver, hvordan ladningshastigheden bremser, når kondensatoren nærmer sig fuld kapacitet.Omvendt under udskrivning falder kondensatorens spænding i henhold til 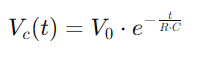 , der fremstiller et lineært fald i lagret energi over tid.Denne proces giver et klart billede af, hvordan energi frigøres fra kondensatoren tilbage i kredsløbet.I AC -applikationer er faseforskellen mellem spænding og strøm, φ, bliver kritisk.Denne forskel beregnet som
, der fremstiller et lineært fald i lagret energi over tid.Denne proces giver et klart billede af, hvordan energi frigøres fra kondensatoren tilbage i kredsløbet.I AC -applikationer er faseforskellen mellem spænding og strøm, φ, bliver kritisk.Denne forskel beregnet som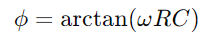 hvor ω Repræsenterer vinkelfrekvens, viser forsinkelsen forårsaget af kondensatoren, som påvirker timingen mellem når strømmen flyder og spændingsændringer over komponenterne.
hvor ω Repræsenterer vinkelfrekvens, viser forsinkelsen forårsaget af kondensatoren, som påvirker timingen mellem når strømmen flyder og spændingsændringer over komponenterne.
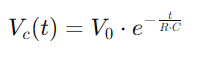 , der fremstiller et lineært fald i lagret energi over tid.Denne proces giver et klart billede af, hvordan energi frigøres fra kondensatoren tilbage i kredsløbet.I AC -applikationer er faseforskellen mellem spænding og strøm, φ, bliver kritisk.Denne forskel beregnet som
, der fremstiller et lineært fald i lagret energi over tid.Denne proces giver et klart billede af, hvordan energi frigøres fra kondensatoren tilbage i kredsløbet.I AC -applikationer er faseforskellen mellem spænding og strøm, φ, bliver kritisk.Denne forskel beregnet som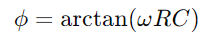 hvor ω Repræsenterer vinkelfrekvens, viser forsinkelsen forårsaget af kondensatoren, som påvirker timingen mellem når strømmen flyder og spændingsændringer over komponenterne.
hvor ω Repræsenterer vinkelfrekvens, viser forsinkelsen forårsaget af kondensatoren, som påvirker timingen mellem når strømmen flyder og spændingsændringer over komponenterne.Generelt grænser og styrer modstanden strømmen af strøm, mens kondensatoren opbevarer og modulerer spændingen.Sammen bestemmer de kredsløbets responskarakteristika, såsom hvor hurtigt det kan oplade og decharge, og de faseskift, der forekommer i vekslende aktuelle scenarier.Denne kombinerede opførsel understøtter de grundlæggende operationer i RC -serien kredsløb, hvilket gør dem integrerede i forskellige elektroniske applikationer.
Grundlæggende ligninger af RC -serien kredsløb
For at forstå opførslen af et RC -serien kredsløb er det vigtigt at starte med de grundlæggende ligninger, der beskriver dens respons på ændringer i indgangsspænding.Antag, at vi har en skiftende indgangsspænding repræsenteret som Vin (T), med spændingen over den modstand, der er mærket som VR (t) og på tværs af kondensatoren som VC (T).I et seriekredsløb, den samme strøm, Det) strømmer gennem både modstanden og kondensatoren.
Anvendelse af Kirchhoffs spændingslov (KVL), der siger, at den samlede spænding omkring enhver lukket sløjfe i et kredsløb skal svare til nul, finder vi, at indgangsspændingen er lig med summen af spændingen over modstanden og kondensatoren:

Spændingen over modstanden kan beregnes ved hjælp af Ohms lov:
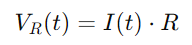
For kondensatoren er spændingen VC (T) relateret til den ladning q (t), den har, givet af:
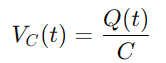
Da strømmen er defineret som gebyrstrømmen, har vi:
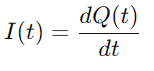
Ved at erstatte Q (t) I ligningen for VC (T)og ved hjælp af afledningen af ladning Det), Vi udleder kernedifferentialligningen for RC -serien kredsløb:

Yderligere udskiftning Q (t) med integralet af Det), vi får:
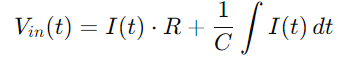
For den nuværende I (T), i betragtning af ændringshastigheden for spænding på tværs af kondensatoren, bruger vi:
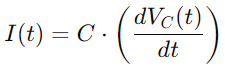
Integrering af alle disse forhold giver os den differentielle ligning, der beskriver spændingen over kondensatoren:
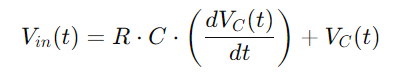
Dette er en første ordens lineær differentiel ligning, der fanger den tidsafhængige ændring af spænding over kondensatoren.Løsning af denne ligning giver os mulighed for præcist at beskrive, hvordan kondensatorspændingen udvikler sig.Denne forståelse er grundlæggende for at analysere både opladnings- og afladningscyklusser af kondensatoren såvel som kredsløbets respons på forskellige frekvenser.Denne omfattende tilgang giver en dyb indsigt i de dynamiske egenskaber ved RC -serien kredsløb.

Figur 6: Spændingsdifferentialligning
Impedans af RC -serien kredsløb
For at omskrive beskrivelsen af et RC-seriekredsløb, med fokus på menneskelig interaktion og en direkte, forenklet forklaring, lad os forbedre de konkrete oplevelser og trin-for-trin-operationer, der er involveret, mens vi opretholder kernemeddelelsen og sammenhængen:
I et RC -serien kredsløb fungerer modstanden og kondensatoren i tandem for at kontrollere strømmen af elektricitet, afgørende, når man beskæftiger sig med skiftende strømme.Kredsløbets samlede impedans, repræsenteret som 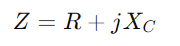 , kombinerer modstanden R og den kapacitive reaktans XC.Det centrale træk ved denne opsætning er, at impedansværdierne for begge komponenter varierer med frekvensændringer.Når frekvensen stiger, falder kondensatorens impedans, hvilket gør det muligt for mere strøm at passere igennem, mens modstanden i det væsentlige forbliver konstant.
, kombinerer modstanden R og den kapacitive reaktans XC.Det centrale træk ved denne opsætning er, at impedansværdierne for begge komponenter varierer med frekvensændringer.Når frekvensen stiger, falder kondensatorens impedans, hvilket gør det muligt for mere strøm at passere igennem, mens modstanden i det væsentlige forbliver konstant.
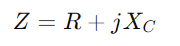 , kombinerer modstanden R og den kapacitive reaktans XC.Det centrale træk ved denne opsætning er, at impedansværdierne for begge komponenter varierer med frekvensændringer.Når frekvensen stiger, falder kondensatorens impedans, hvilket gør det muligt for mere strøm at passere igennem, mens modstanden i det væsentlige forbliver konstant.
, kombinerer modstanden R og den kapacitive reaktans XC.Det centrale træk ved denne opsætning er, at impedansværdierne for begge komponenter varierer med frekvensændringer.Når frekvensen stiger, falder kondensatorens impedans, hvilket gør det muligt for mere strøm at passere igennem, mens modstanden i det væsentlige forbliver konstant.Impedansen, betegnet som Z og målt i ohm (ω) spiller en kritisk rolle i bestemmelsen af, hvordan kredsløbet reagerer på skiftevis strøm.Ligesom i RL -serien kredsløb, modstanden R og kapacitiv reaktans xC af et RC -kredsløb danner en trekant kendt som impedanstrekanten.Denne trekant relaterer tæt på spændingstrekanten, og ved at anvende Pythagorean -sætningen kan du beregne kredsløbets samlede impedans.

Figur 7: RC -serien Circuit Calculation Formula
Når det kommer til praktiske applikationer, skal du overveje hovedtelefoner, der bruger disse principper.Højimpedanshovedtelefoner, ofte over 200 ohm, bruges typisk med desktopcomputere, strømforstærkere og professionelt lydudstyr.Disse modeller med høj impedans stemmer godt overens med outputfunktionerne inden for professionel kvalitet elektronik.Når du bruger disse hovedtelefoner, er det vigtigt at justere volumen gradvist for at undgå overbelastning og beskadigelse af de delikate interne komponenter, såsom stemmespolen.
Omvendt foretrækkes hovedtelefoner med lav impedans, normalt under 50 ohm, til bærbare enheder som CD-afspillere, MD-afspillere eller MP3-afspillere.Disse hovedtelefoner kræver mindre strøm til at levere lyd af høj kvalitet, hvilket gør dem ideelle til mobilbrug.De kræver dog også omhyggelig opmærksomhed på følsomhedsniveauer for at sikre optimal ydelse og forhindre skade på hovedtelefoner eller hørelse.

Figur 8: Impedansdiagram over RC -serien kredsløb
Adgangs- og analyseprocedurer for RC -serien kredsløb
Adgang måler, hvor let et RC -serien kredsløb kan udføre elektricitet, beregnet som det inverse af impedans ( ).Denne værdi integrerer både modstanden (R) og reaktansen (X) af kredsløbet.Modstanden modsætter sig den nuværende strømning ved at konvertere elektrisk energi til varme, mens reaktans gemmer energi midlertidigt i kredsløbet.
).Denne værdi integrerer både modstanden (R) og reaktansen (X) af kredsløbet.Modstanden modsætter sig den nuværende strømning ved at konvertere elektrisk energi til varme, mens reaktans gemmer energi midlertidigt i kredsløbet.
 ).Denne værdi integrerer både modstanden (R) og reaktansen (X) af kredsløbet.Modstanden modsætter sig den nuværende strømning ved at konvertere elektrisk energi til varme, mens reaktans gemmer energi midlertidigt i kredsløbet.
).Denne værdi integrerer både modstanden (R) og reaktansen (X) af kredsløbet.Modstanden modsætter sig den nuværende strømning ved at konvertere elektrisk energi til varme, mens reaktans gemmer energi midlertidigt i kredsløbet.At beregne adgang
Start med at skrive impedansen 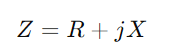 , hvor R står for modstand, X til reaktans og j er den imaginære enhed.Brug formlen y = 1/((R + JX).Denne operation involverer komplekse tal og giver os
, hvor R står for modstand, X til reaktans og j er den imaginære enhed.Brug formlen y = 1/((R + JX).Denne operation involverer komplekse tal og giver os 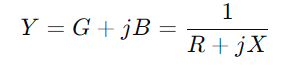 .Her, G er ledningsevnen (faktisk strømstrømningsevne) og B er følsomheden (kredsløbets evne til at reagere på ændringer i strøm).
.Her, G er ledningsevnen (faktisk strømstrømningsevne) og B er følsomheden (kredsløbets evne til at reagere på ændringer i strøm).
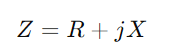 , hvor R står for modstand, X til reaktans og j er den imaginære enhed.Brug formlen y = 1/((R + JX).Denne operation involverer komplekse tal og giver os
, hvor R står for modstand, X til reaktans og j er den imaginære enhed.Brug formlen y = 1/((R + JX).Denne operation involverer komplekse tal og giver os 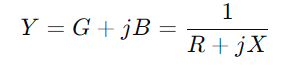 .Her, G er ledningsevnen (faktisk strømstrømningsevne) og B er følsomheden (kredsløbets evne til at reagere på ændringer i strøm).
.Her, G er ledningsevnen (faktisk strømstrømningsevne) og B er følsomheden (kredsløbets evne til at reagere på ændringer i strøm).
Figur 9: Serie RC Circuit Impedance Calculator
Denne beregning afslører ikke kun kredsløbets ledningsevne, men også dets dynamiske responskarakteristika, afgørende for AC -kredsløbsanalyse.Konduktans og følsomhed, samlet, indikerer, hvordan kredsløbet passerer strømmen, og hvordan det gemmer og frigiver energi.

Figur 10: Fasevinkelformel
Praktisk anvendelse
Ingeniører bruger adgangsværdier for at forbedre kredsløbsdesign, især i højfrekvente applikationer, såsom radiofrekvenskredsløb.Justering af adgang hjælper med at matche impedans, reducere signalreflektion og øge transmissionseffektiviteten.
Ved at studere adgangsrespons kan ingeniører vurdere og forudsige kredsløbsydelse under forskellige forhold som frekvensrespons, stabilitet og følsomhed.Udstyr med et oscilloskop og en signalgenerator til at måle kredsløbets spænding og strøm ved forskellige frekvenser.Fokuser især på cutoff -frekvensen for at teste teoretiske forudsigelser og validere dem mod praktiske observationer.For AC -kredsløb skal du starte med at bestemme reaktansen (XC) af kondensatoren med 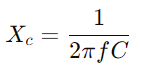 , hvor f er signalfrekvensen.Beregn den samlede impedans
, hvor f er signalfrekvensen.Beregn den samlede impedans og derefter optagelse
og derefter optagelse  .
.
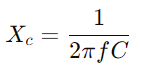 , hvor f er signalfrekvensen.Beregn den samlede impedans
, hvor f er signalfrekvensen.Beregn den samlede impedans og derefter optagelse
og derefter optagelse  .
.Analyser faseforskellen ved hjælp af 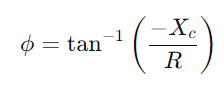 at forstå signalformændring.Undersøg, hvordan kredsløbet håndterer forskellige frekvenser, især og bemærker adfærden ved cutoff -frekvensen
at forstå signalformændring.Undersøg, hvordan kredsløbet håndterer forskellige frekvenser, især og bemærker adfærden ved cutoff -frekvensen 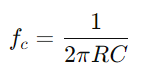 , hvor kredsløbet skifter fra at passere til blokeringssignaler.Evaluering af, hvordan impedans og faseforskel varierer med frekvens, er afgørende for at designe effektive filtre og signalprocessorer.Diskuter, hvordan frekvensselektivitet, faseskift og signaldæmpning på grund af kredsløbets egenskaber påvirker praktiske anvendelser som filtrering og elektronisk tuning.
, hvor kredsløbet skifter fra at passere til blokeringssignaler.Evaluering af, hvordan impedans og faseforskel varierer med frekvens, er afgørende for at designe effektive filtre og signalprocessorer.Diskuter, hvordan frekvensselektivitet, faseskift og signaldæmpning på grund af kredsløbets egenskaber påvirker praktiske anvendelser som filtrering og elektronisk tuning.
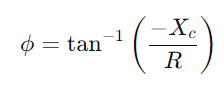 at forstå signalformændring.Undersøg, hvordan kredsløbet håndterer forskellige frekvenser, især og bemærker adfærden ved cutoff -frekvensen
at forstå signalformændring.Undersøg, hvordan kredsløbet håndterer forskellige frekvenser, især og bemærker adfærden ved cutoff -frekvensen 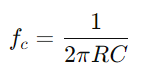 , hvor kredsløbet skifter fra at passere til blokeringssignaler.Evaluering af, hvordan impedans og faseforskel varierer med frekvens, er afgørende for at designe effektive filtre og signalprocessorer.Diskuter, hvordan frekvensselektivitet, faseskift og signaldæmpning på grund af kredsløbets egenskaber påvirker praktiske anvendelser som filtrering og elektronisk tuning.
, hvor kredsløbet skifter fra at passere til blokeringssignaler.Evaluering af, hvordan impedans og faseforskel varierer med frekvens, er afgørende for at designe effektive filtre og signalprocessorer.Diskuter, hvordan frekvensselektivitet, faseskift og signaldæmpning på grund af kredsløbets egenskaber påvirker praktiske anvendelser som filtrering og elektronisk tuning.Denne tilgang nedbryder de operationelle processer i håndterbare trin og beriger brugerens forståelse med praktisk indsigt i håndtering og analyse af RC -seriekredsløb.

Figur 11: Karakteristika for RC -serien kredsløb
Phasor -diagram over RC -serien kredsløb
I et RC -serien kredsløb deler alle elementer den samme strøm på grund af deres seriens konfiguration.Denne ensartede strøm fungerer som en basislinje for vores fasordiagram, som hjælper med at visualisere forholdet mellem forskellige spændinger og strømme i kredsløbet.Lad os udpege denne nuværende jeg som referencephasor, placeret ved nul grader på diagrammet.I diagrammet, strømmen jeg indstilles vandret til højre og etablerer nul-graders referencelinie.Spændingen over modstanden (UR) er i fase med strømmen, fordi modstande ikke forårsager nogen faseskift.Således, UR trækkes som en vandret vektor i samme retning som jeg, der strækker sig fra oprindelsen.

Figur 12: RC -serien Circuit Phasor Diagram
I modsætning hertil, spændingen over kondensatoren (UC) fører strømmen med 90 grader på grund af den kapacitive egenskab ved at forsinke den nuværende fase.Denne spænding er repræsenteret af en lodret vektor, der peger opad, startende fra spidsen af UR Vector.Den samlede spænding U i kredsløbet er vektorsummen af U Rand UC.Dette beløb danner en højre trekant med UR og UC som henholdsvis de tilstødende og modsatte sider.Hypotenusen af denne trekant, der strækker sig fra oprindelsen til spidsen af UC Vector, repræsenterer U.
Den sinusformede strøm gennem kredsløbet er givet ved synd (ωt), hvor IM er den maksimale aktuelle amplitude og ω er vinkelfrekvensen.Derfor er spændingen over modstanden 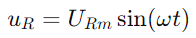 , der spejler den aktuelle bølgeform.Spændingen over kondensatoren er givet af
, der spejler den aktuelle bølgeform.Spændingen over kondensatoren er givet af  , hvilket indikerer en faseskift på -90 ° (eller 90 grader foran strømmen).Phasor -diagramets højre trekant præciserer det
, hvilket indikerer en faseskift på -90 ° (eller 90 grader foran strømmen).Phasor -diagramets højre trekant præciserer det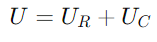 er ikke kun i størrelse, men også i faseforhold med terminalspændingsvektoren (U) færdiggørelse af trekanten.
er ikke kun i størrelse, men også i faseforhold med terminalspændingsvektoren (U) færdiggørelse af trekanten.
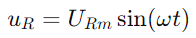 , der spejler den aktuelle bølgeform.Spændingen over kondensatoren er givet af
, der spejler den aktuelle bølgeform.Spændingen over kondensatoren er givet af  , hvilket indikerer en faseskift på -90 ° (eller 90 grader foran strømmen).Phasor -diagramets højre trekant præciserer det
, hvilket indikerer en faseskift på -90 ° (eller 90 grader foran strømmen).Phasor -diagramets højre trekant præciserer det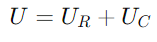 er ikke kun i størrelse, men også i faseforhold med terminalspændingsvektoren (U) færdiggørelse af trekanten.
er ikke kun i størrelse, men også i faseforhold med terminalspændingsvektoren (U) færdiggørelse af trekanten.
Figur 13: Spændingsfasordiagram over RC -serien kredsløb
Nøglepunkter i analyse af serier RC -kredsløb
Impedans i serie RC -kredsløb, repræsenteret som Z, kombinerer modstand (R) og den reaktive virkning af kapacitans i en enkelt måling, der varierer med signalfrekvens.Det udtrykkes matematisk som 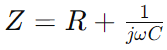 , hvor ω er vinkelfrekvensen og C er kapacitansen.Her, R udgør den virkelige del af impedansen og
, hvor ω er vinkelfrekvensen og C er kapacitansen.Her, R udgør den virkelige del af impedansen og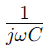 Repræsenterer den imaginære del, hvilket indikerer, hvordan kondensatoren påvirker kredsløbet.
Repræsenterer den imaginære del, hvilket indikerer, hvordan kondensatoren påvirker kredsløbet.
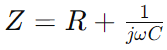 , hvor ω er vinkelfrekvensen og C er kapacitansen.Her, R udgør den virkelige del af impedansen og
, hvor ω er vinkelfrekvensen og C er kapacitansen.Her, R udgør den virkelige del af impedansen og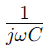 Repræsenterer den imaginære del, hvilket indikerer, hvordan kondensatoren påvirker kredsløbet.
Repræsenterer den imaginære del, hvilket indikerer, hvordan kondensatoren påvirker kredsløbet.Den måde, impedans ændrer sig med frekvens, er central til anvendelse af serier RC -kredsløb i filtrering af applikationer.Ved lavere frekvenser udviser kredsløbet højere impedans, hvilket effektivt blokerer for disse frekvenser.Omvendt falder impedansen ved højere frekvenser, hvilket gør det muligt for disse frekvenser at passere mere frit.Denne opførsel gør serien RC-kredsløb ideelle til opgaver som filtrering af uønsket lavfrekvent støj eller passerer højfrekvente signaler.

Figur 14: Impedansvektordiagram over RC -serien kredsløb
Konklusion
Fra filtrering af uønskede frekvenser til udformning af signalresponser er RC -serien kredsløb medvirkende til en lang række elektroniske funktioner.Ved at forstå de underliggende principper, såsom impedans, fasorforhold og den frekvensafhængige opførsel af disse kredsløb, er ingeniører og designere udstyret til at håndtere løsninger, der effektivt styrer signalintegritet i komplekse elektroniske systemer.Den detaljerede undersøgelse af disse kredsløb, understøttet af matematisk analyse og visuelle repræsentationer som fasordiagrammer, giver en omfattende indsigt, der er vigtig for alle, der ønsker at uddybe deres forståelse af elektronisk kredsløbsdynamik eller for at forbedre deres praktiske færdigheder inden for kredsløbsdesign og fejlfinding.
Ofte stillede spørgsmål [FAQ]
1. Hvad er princippet om RC -kredsløb?
Princippet om et RC (modstandskapacitor) kredsløb drejer sig om opladnings- og afladningsprocesserne for kondensatoren gennem modstanden.I dette kredsløb interagerer kondensatorens evne til at opbevare og frigive elektrisk energi med modstanden, der styrer den hastighed, hvormed kondensatoren oplades eller udledes.
2. Hvorfor fører et RC -kredsløbsstrøm?
I et RC -kredsløb fører strømmen spændingen over kondensatoren, fordi kondensatoren er nødt til at begynde at oplade, før dens spænding kan stige.Da strømmen strømmer ind i kondensatoren for at oplade den, når de aktuelle toppe, før spændingen over kondensatoren når sit maksimum.Denne effekt forårsager et faseskift, hvor den aktuelle fase fører spændingen fase med op til 90 grader, afhængigt af frekvensen af indgangssignalet.
3. Hvordan ændres spænding i et RC -kredsløb?
Spændingsændringen i et RC -kredsløb under opladning er beskrevet af en eksponentiel funktion.Når der påføres en spænding, øges spændingen over kondensatoren oprindeligt hurtigt, og bremser derefter, når den nærmer sig forsyningsspændingen.Matematisk udtrykkes dette som 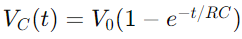 , hvor VC(t) er spændingen over kondensatoren på tidspunktet t, v0 er forsyningsspændingen, og RC er tidskonstantens tidskonstant, der bestemmer, hvor hurtigt kondensatoren lades.Omvendt, under afladning, falder spændingen over kondensatoren eksponentielt efter ligningen
, hvor VC(t) er spændingen over kondensatoren på tidspunktet t, v0 er forsyningsspændingen, og RC er tidskonstantens tidskonstant, der bestemmer, hvor hurtigt kondensatoren lades.Omvendt, under afladning, falder spændingen over kondensatoren eksponentielt efter ligningen 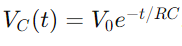 .
.
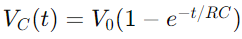 , hvor VC(t) er spændingen over kondensatoren på tidspunktet t, v0 er forsyningsspændingen, og RC er tidskonstantens tidskonstant, der bestemmer, hvor hurtigt kondensatoren lades.Omvendt, under afladning, falder spændingen over kondensatoren eksponentielt efter ligningen
, hvor VC(t) er spændingen over kondensatoren på tidspunktet t, v0 er forsyningsspændingen, og RC er tidskonstantens tidskonstant, der bestemmer, hvor hurtigt kondensatoren lades.Omvendt, under afladning, falder spændingen over kondensatoren eksponentielt efter ligningen 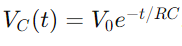 .
. OM OS
Kundetilfredshed hver gang.Gensidig tillid og fælles interesser.
OM OS
Kundetilfredshed hver gang.Gensidig tillid og fælles interesser.
Funktionstest.De højeste omkostningseffektive produkter og den bedste service er vores evige engagement.
Varm artikel
- Er CR2032 og CR2016 udskiftelige
- MOSFET: Definition, arbejdsprincip og udvælgelse
- Relæinstallation og test, fortolkning af relæ -ledningsdiagrammer
- CR2016 vs. CR2032 Hvad er forskellen
- NPN vs. PNP: Hvad er forskellen?
- ESP32 vs STM32: Hvilken mikrokontroller er bedre for dig?
- LM358 Dual Operational Amplifier Comprehensive Guide: Pinouts, kredsløbsdiagrammer, ækvivalenter, nyttige eksempler
- CR2032 vs DL2032 vs CR2025 sammenligningsvejledning
- Forståelse af forskellene ESP32 og ESP32-S3 teknisk og præstationsanalyse
- Detaljeret analyse af RC -serien kredsløb
 Dybdegående analyse af 1N4148 Dioder: Driftstilstande, specifikationer og brugsscenarier
Dybdegående analyse af 1N4148 Dioder: Driftstilstande, specifikationer og brugsscenarier
2024-05-08
 Forståelse af typer og anvendelser af dynamiske og positive forskydningspumper
Forståelse af typer og anvendelser af dynamiske og positive forskydningspumper
2024-05-07
Hot delnummer
 GRM0335C1E150GA01J
GRM0335C1E150GA01J GRM033R71E222MA12J
GRM033R71E222MA12J GCM31A7U2J391JX01D
GCM31A7U2J391JX01D GQM1555C2DR75BB01D
GQM1555C2DR75BB01D 18085A821JAT2A
18085A821JAT2A F970J476MCA
F970J476MCA MAX120EWG
MAX120EWG MMZ1608Y102BTA00
MMZ1608Y102BTA00 ATMEGA48A-AUR
ATMEGA48A-AUR ATSAM3S1AB-AUR
ATSAM3S1AB-AUR
- FP50R12KT3
- VI-BW0-01
- AD8674ARUZ
- CDCV855IPWR
- LTC2055CMS8#PBF
- UCC2809P-1
- XC2VP40-5FFG1152I
- NCP1271D100R2G
- STM32F301C8T6TR
- ADG4612BCPZ
- ADV7613WBBCZ-RL
- AM29205-16KC
- AM29LV320DB-120EI
- AM3715CBCDNB
- AR9223-AC1A
- BC817-40W
- HD6412392TE20
- IDT70V631S12PRF
- MAX6650EUB
- MC146805E2CFN
- NAND01GR3B2CZF5
- NHPXA270C0C416
- RH80532NC009256
- S-8424AARFT-TB-G
- SAF-XC866-2FRI
- SC14438A5M64VYX
- SC4809AIMSTR
- TC7WZ74FU
- TMP95FY64F
- XC4028XLA-09BG256C
- CMM0333-AK-00LT
- G5118P8UF
- RTL8368S
- SAK-C167CR-4RMHA
- YAS532B-PZE7
- LM2904BIPWR
- THVD1419DT
- US1BW
- B43310-S5338-M